Энтропийный метод мониторинга реализации экономических стратегий
Поясним методику построения диаграммы Лоренца для произвольной последовательности {Gi} из N чисел на конкретном примере. В качестве исходной числовой последовательности возьмем ряд из N = 5 чисел: 600, 70, 100, 200, 30. Прежде всего упорядочим этот ряд чисел в порядке их возрастания: G1 = 30; G2 = 70; G3 = 100; G4 =200; G5 = 600 и рассчитаем ряд частичных сумм {Sn} «нарастающим итогом» по формуле:
Sn = G1 +… + Gn (1 ≤ n ≤ N).
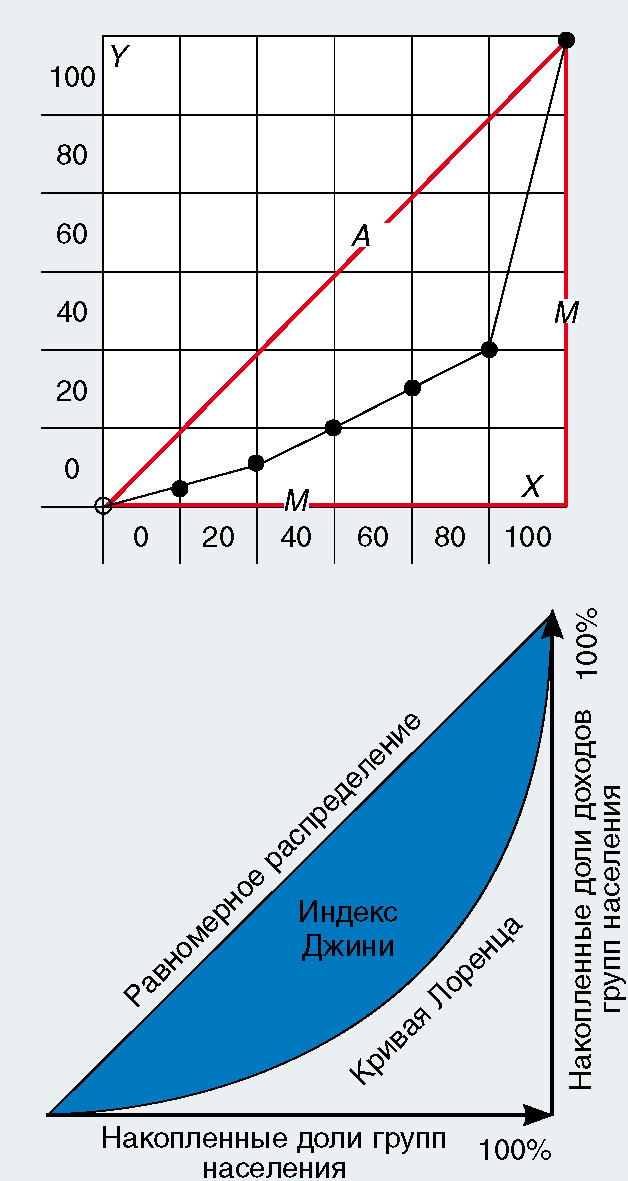
Т.е. S1 = G1 = 30, S2 = 30 + 70 = 100,… S5 = 1000. На диаграмме Лоренца (рис. 3) значения, откладываемые по вертикальной оси Y, определяются нормированием частичных сумм Sn на сумму всех чисел рассматриваемой последовательности (yn = Sn / SN) в процентах или в относительных единицах. Соответствующие значения координат по горизонтальной оси X определяются аналогичным способом (xn = n / N), где последовательность «номеров» (позиций) n элементов систем берется в порядке возрастания элементов (кумулятивная кривая). В итоге, откладывая полученные точки (xn, yn) внутри квадрата со сторонами, равными единице (или 100%), получаем диаграмму Лоренца для исследуемой последовательности (рис. 3).
Рисунок 3
Диаграммы Лоренца для произвольного числового ряда и для двух предельных по неравномерности рядов
Отметим, что описанный подход позволяет нанести в виде диаграмм Лоренца любые числовые последовательности. Можно сказать, что диаграмма Лоренца представляет собой своеобразное «ранговое распределение».
Использование процедуры упорядочения исходных последовательностей чисел по их возрастанию позволяет разместить все диаграммы Лоренца между двумя предельными конфигурациями: линией А, отражающей абсолютно равномерное распределение («Анархия»), и линией М, характеризующей абсолютно неравномерное распределение («Монархия»).
Имея набор диаграмм Лоренца для различных моментов времени состояния выделенной экономической системы, можно судить о предпочтительных распределениях, позволяющих сделать вывод о положительном или негативном характере происходящих изменений.
Примеры состояний экономических систем с предпочтительным характером распределения ресурсов
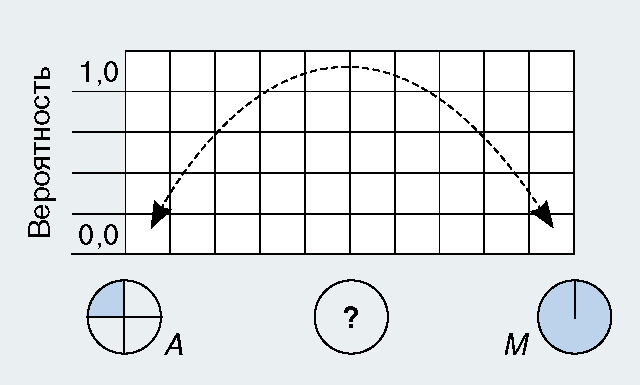
Несложно убедиться в том, что указанные предельные варианты (А и М) достаточно редко встречаются в экономической практике. Принимая во внимание малую вероятность появления указанных предельных случаев и их граничное положение в иерархии всевозможных распределений, можно предположить, что существует промежуточный предпочтительный (наиболее вероятный) вариант распределения (рис. 4). Ниже даны примеры такого рода распределений.
Рисунок 4
Гипотеза о существовании предпочтительных числовых последовательностей
Настоящая Политика конфиденциальности персональных данных действует в отношении всех персональных данных, которые Компания «ТЕКОРА» может получить от Вас во время использования Вами сайтов компании.
Заполняя форму на сайте https://tekora.ru/ и других веб-сайтах Компании «ТЕКОРА», которые собирают данные и ссылаются на эти условия, Вы даете свое добровольное согласие Компании «ТЕКОРА» на обработку нижеследующих персональных данных с применением автоматизированных средств обработки или без таковых: фамилия, имя, отчество; место работы, наименование занимаемой должности; адрес электронной почты; номер контактного телефона.
Предоставляя Компании «ТЕКОРА» информацию, необходимую для инициирования дальнейшего взаимодействия, Вы выражаете согласие на ее использование в соответствии с настоящей Политикой.
Если Вы не согласны с приведенными в настоящем документе условиями, пожалуйста, не используйте данные веб-сайты и не заполняйте формы запроса информации.
Компания «ТЕКОРА» означает:
АО «ТЕКОРА», Юридический адрес: 119633, г. Москва, муниципальный округ Ново-Переделкино, Боровское ш., дом. 18, корп. 3, этаж 1, помещение 1, комната 5, офис 40.
Почтовый адрес: 117393, Москва, ул. Профсоюзная, д.56, оф. 15оф 19-23.
Под обработкой персональных данных понимаются действия, предусмотренные законодательством Российской Федерации, в том числе Федеральным законом от 27.07.2006 N 152-ФЗ. "О персональных данных".
Предоставляя свои персональные данные Вы соглашаетесь на их обработку, включая сбор, запись, систематизацию, накопление, хранение, уточнение (обновление, изменение), извлечение, использование, передачу, обезличивание, удаление, уничтожение Компанией «ТЕКОРА» в целях обработки Ваших заказов и запросов, для осуществления деятельности по продвижению товаров, работ, услуг или объектов интеллектуальной собственности на рынке путем осуществления прямых контактов с Вами с помощью средств связи, оценки и анализа сайта, анализа покупательских особенностей и предоставления персональных рекомендаций; информирования Вас об акциях, скидках и специальных предложениях посредством электронных рассылок, а также в целях связи с Вами (по электронной почте и/или телефону).
Предоставляя Компании «ТЕКОРА» свои персональные данные, вы можете быть уверены, что они не будут предоставляться третьим сторонам, за исключением случаев, когда это требуется в интересах деловых отношений между Вами и Компанией «ТЕКОРА». В некоторых случаях Компания «ТЕКОРА» обязана передавать Ваши персональные данные третьим лицам в связи с требованиями применимого законодательства. Например, это может быть в случае, когда существуют основания подозревать в совершении преступления или неправомерном использовании веб-сайта Компании «ТЕКОРА».
Вы можете в любой момент отказаться от получения сообщений по электронной почте, однако это не затрагивает передачу сообщений по электронной почте, которые требуются в целях реализации деловых отношений между Вами и компанией «ТЕКОРА».
Указанные веб-сайты содержат несколько ссылок на компании, с которыми Компания «ТЕКОРА» поддерживает деловые отношения. Компания «ТЕКОРА» не несет ответственность за соответствие требованиям по защите персональных данных в отношении использования веб-сайтов партнеров Компании «ТЕКОРА». Для получения информации о защите данных при посещении этих сайтов, пожалуйста, ознакомьтесь с политиками конфиденциальности на веб-сайтах соответствующих компаний.
Персональные данные, собираемые Компанией «ТЕКОРА», хранятся на защищенных серверах. Доступ разрешен только ограниченному числу уполномоченных лиц, которые нуждаются в нем для того, чтобы управлять веб-сайтами Компании «ТЕКОРА» или обеспечить их надлежащую функциональность, особенно в части технической поддержки.
Настоящим согласием Вы подтверждаете, что являетесь субъектом предоставляемых персональных данных, а также подтверждаете достоверность предоставляемых данных.
Компания «ТЕКОРА» предпринимает разумные меры для поддержания точности и актуальности имеющихся у нее персональных данных, а также удаления устаревших и других недостоверных или излишних персональных данных, тем не менее, Вы несёте ответственность за предоставление достоверных сведений, а также за обновление предоставленных данных в случае каких-либо изменений.
Вы можете в любой момент изменить (обновить, дополнить) предоставленную Вами персональную информацию или её часть, а также параметры её конфиденциальности путем обращения в Компанию «ТЕКОРА».
Обращаем внимание, что данное согласие предоставляется исключительно на добровольной основе. Настоящее согласие действует в течение 20 лет и может быть отозвано Вами в любое время, путем направления Компании «ТЕКОРА» заказного письма с уведомлением о вручении по адресам для корреспонденции Компании «ТЕКОРА», которые указаны в настоящем тексте согласия.
Все предложения или вопросы по поводу настоящей Политики следует сообщать Компании «ТЕКОРА» по телефону +7(495) 336-16-19 или по адресу электронной почты office@tekora.ru.
Политика конфиденциальности может обновляться в связи с возможными поправками к закону или изменениями внутренних процессов Компании «ТЕКОРА».
Последнее обновление: 1 марта 2021 г.