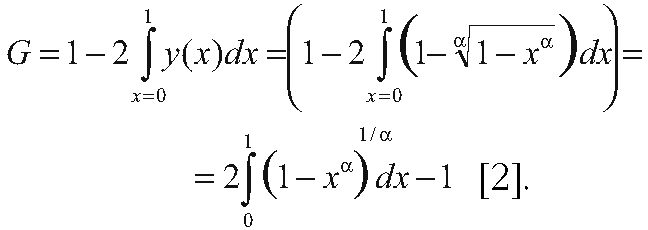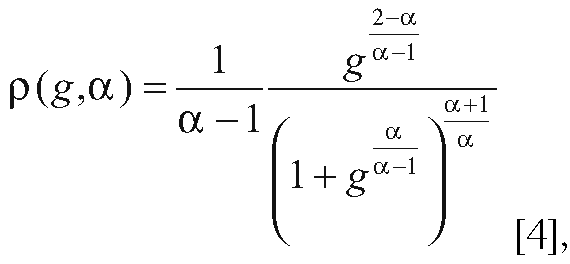Энтропийный метод мониторинга реализации экономических стратегий
Аппроксимация диаграмм Лоренца однопараметрической функцией
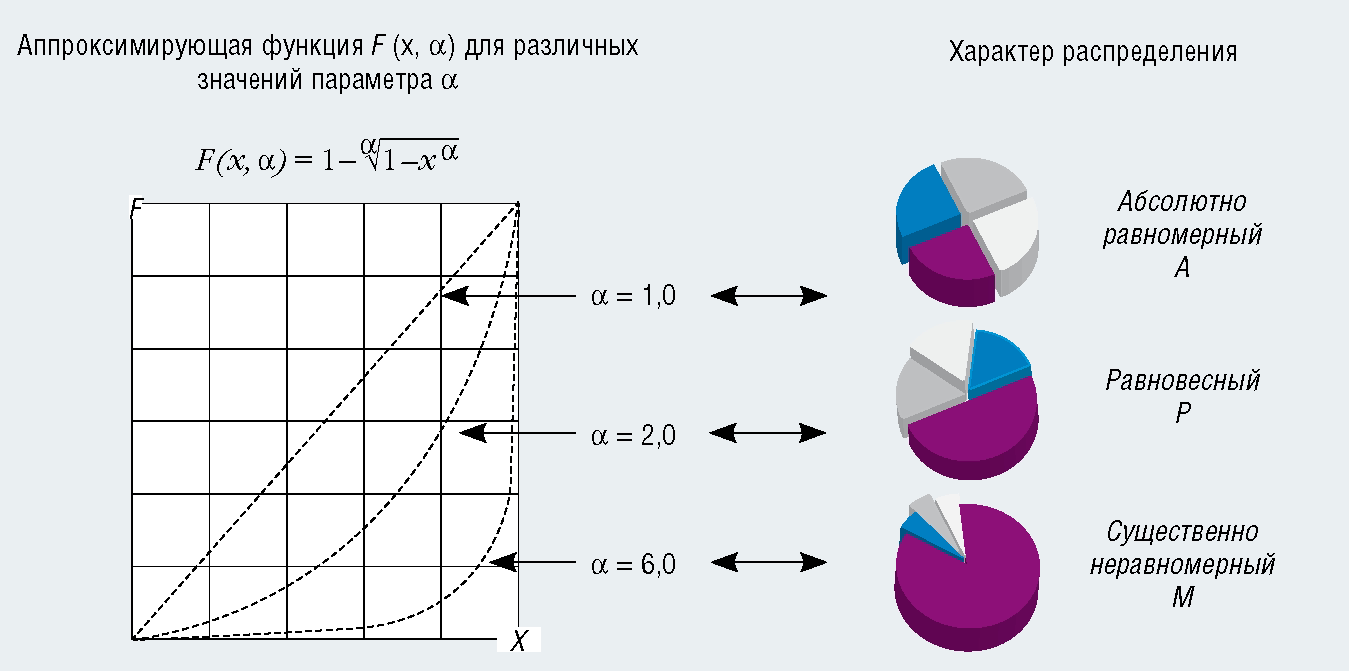
Для дальнейшего анализа удобно аппроксимировать диаграмму Лоренца однопараметрической функцией y = F(x, α):
Здесь параметр α может изменяться от 1 до ∞. При α = 1 функция F(x, α) = x и характеризует равномерное распределение (А). При α = 2 функция F(x, α) совпадает с фрагментом окружности, а при α >> 2 – описывает существенно неравномерное распределение, приближающееся к М (рис. 9).
Рисунок 9
Функция F(x, α) для различных значений параметра α
Напомним, что отношение площади, ограниченной кривой Лоренца и линией абсолютного равенства А (рис. 3), к площади треугольника, лежащей под линией абсолютного равенства А, называют коэффициентом Джини (Gini coefficient) – G. Иногда индексом Джини называют коэффициент Джини, выраженный в процентах. Коэффициентом (индексом) Джини обычно характеризуют степень расслоения общества данной страны или региона по отношению к какому-либо изучаемому признаку (как правило, по уровню годового дохода). В этом случае коэффициент Джини именуют индексом концентрации доходов. Он принимает значения от 0 до 1 (0 – в случае абсолютного равенства в распределении доходов, 1 – в случае абсолютного неравенства). Возрастание индекса Джини указывает на рост неравенства.
Аппроксимация фактических диаграмм Лоренца функцией F(x, α) позволяет найти связь параметра α с коэффициентом Джини, то есть использовать вместо коэффициента Джини параметр α и упорядочить числовые последовательности по степени неравномерности (характера) распределения последовательностей чисел. Согласно определению коэффициента Джини при достаточно большом числе N, имеем:
В общем случае этот интеграл аналитически не берется и определяется численными методами. В частном случае при α = 2, когда диаграмма Лоренца совпадает с фрагментом окружности, имеем G = π/2 – 1 ≈ 0,57. При α < 2 коэффициент Джини меньше 0,57, а при α > 2 получим G > 0,57.
По данным (9, 10), индекс Джини, рассчитанный по годовому доходу жителей, для Москвы равен 0,58, для России – более 0,41. Для ряда стран Европы и Австралии G = 0,25 – 0,3, для США – около 0,5, а для некоторых стран Африки и Латинской Америки индекс Джини превышает 0,6.
Энтропия числовых последовательностей
Весьма продуктивным оказался подход, опирающийся на физические методы определения состояния сложных систем с помощью энтропии. Энтропия характеризует вероятность состояния системы. У И.Р. Пригожина и Дилипа Кондепуди по этому поводу сказано:
«В обычной механике обычными переменными являются координаты и импульсы. У нас же основной переменной будет статистическая функция распределения ρ, с помощью которой можно вычислять средние значения любых функций координат и импульсов. Таким образом, можно сказать, что знание ρ обеспечивает полное знание «состояния» системы» (11).
При известной плотности распределения вероятностей ρ(g, α) некоторой непрерывной числовой последовательности, такой, что ρ(g, α)dg есть вероятность попадания относительной величины ресурса g = Gn / G* = GnN / SN в интервал (g, g + dg), энтропия определяется интегралом:
Здесь величина g является величиной ресурса, приведенной к средней величине ресурса G* = SN / N, т.е. нормирована на величину SN / N.
В нашей работе «Статистические функции распределения ресурсов в экономике», на которую мы ссылались выше, показано, что для однопараметрического распределения числовой последовательности в виде [1] плотность вероятности определяется выражением:
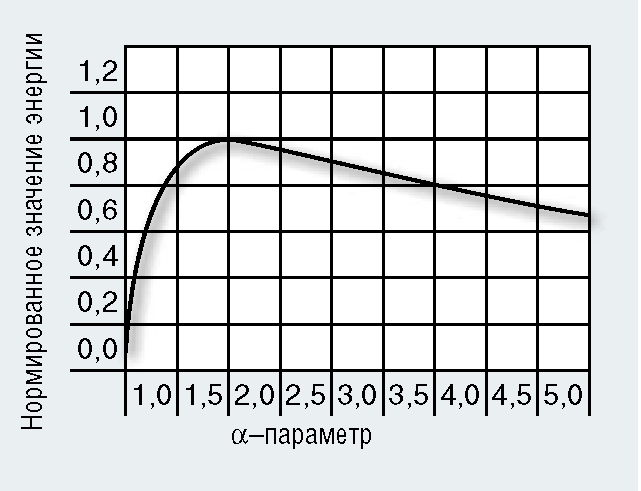
подстановка которого в выражение [3] дает искомую зависимость энтропии системы от параметра распределения α. Как следует из рис. 10, зависимость энтропии от параметра α, определяющего характер диаграммы Лоренца, имеет максимум в окрестности α ≈ 1,8. Следовательно, можно утверждать, что среди числовых последовательностей, описывающих распределение ресурсов в выделенной произвольной экономической системе, есть предпочтительные последовательности или предпочтительные состояния экономической системы, при которых энтропия [3] максимальна. Интересно, что существование оптимального распределения никак не связано с природой рассматриваемого распределения, т.е. обладает некоей универсальностью.
Рисунок 10
Зависимость нормированной энтропии числовой последовательности от характера распределения α числовой последовательности
Настоящая Политика конфиденциальности персональных данных действует в отношении всех персональных данных, которые Компания «ТЕКОРА» может получить от Вас во время использования Вами сайтов компании.
Заполняя форму на сайте https://tekora.ru/ и других веб-сайтах Компании «ТЕКОРА», которые собирают данные и ссылаются на эти условия, Вы даете свое добровольное согласие Компании «ТЕКОРА» на обработку нижеследующих персональных данных с применением автоматизированных средств обработки или без таковых: фамилия, имя, отчество; место работы, наименование занимаемой должности; адрес электронной почты; номер контактного телефона.
Предоставляя Компании «ТЕКОРА» информацию, необходимую для инициирования дальнейшего взаимодействия, Вы выражаете согласие на ее использование в соответствии с настоящей Политикой.
Если Вы не согласны с приведенными в настоящем документе условиями, пожалуйста, не используйте данные веб-сайты и не заполняйте формы запроса информации.
Компания «ТЕКОРА» означает:
АО «ТЕКОРА», Юридический адрес: 119633, г. Москва, муниципальный округ Ново-Переделкино, Боровское ш., дом. 18, корп. 3, этаж 1, помещение 1, комната 5, офис 40.
Почтовый адрес: 117393, Москва, ул. Профсоюзная, д.56, оф. 15оф 19-23.
Под обработкой персональных данных понимаются действия, предусмотренные законодательством Российской Федерации, в том числе Федеральным законом от 27.07.2006 N 152-ФЗ. "О персональных данных".
Предоставляя свои персональные данные Вы соглашаетесь на их обработку, включая сбор, запись, систематизацию, накопление, хранение, уточнение (обновление, изменение), извлечение, использование, передачу, обезличивание, удаление, уничтожение Компанией «ТЕКОРА» в целях обработки Ваших заказов и запросов, для осуществления деятельности по продвижению товаров, работ, услуг или объектов интеллектуальной собственности на рынке путем осуществления прямых контактов с Вами с помощью средств связи, оценки и анализа сайта, анализа покупательских особенностей и предоставления персональных рекомендаций; информирования Вас об акциях, скидках и специальных предложениях посредством электронных рассылок, а также в целях связи с Вами (по электронной почте и/или телефону).
Предоставляя Компании «ТЕКОРА» свои персональные данные, вы можете быть уверены, что они не будут предоставляться третьим сторонам, за исключением случаев, когда это требуется в интересах деловых отношений между Вами и Компанией «ТЕКОРА». В некоторых случаях Компания «ТЕКОРА» обязана передавать Ваши персональные данные третьим лицам в связи с требованиями применимого законодательства. Например, это может быть в случае, когда существуют основания подозревать в совершении преступления или неправомерном использовании веб-сайта Компании «ТЕКОРА».
Вы можете в любой момент отказаться от получения сообщений по электронной почте, однако это не затрагивает передачу сообщений по электронной почте, которые требуются в целях реализации деловых отношений между Вами и компанией «ТЕКОРА».
Указанные веб-сайты содержат несколько ссылок на компании, с которыми Компания «ТЕКОРА» поддерживает деловые отношения. Компания «ТЕКОРА» не несет ответственность за соответствие требованиям по защите персональных данных в отношении использования веб-сайтов партнеров Компании «ТЕКОРА». Для получения информации о защите данных при посещении этих сайтов, пожалуйста, ознакомьтесь с политиками конфиденциальности на веб-сайтах соответствующих компаний.
Персональные данные, собираемые Компанией «ТЕКОРА», хранятся на защищенных серверах. Доступ разрешен только ограниченному числу уполномоченных лиц, которые нуждаются в нем для того, чтобы управлять веб-сайтами Компании «ТЕКОРА» или обеспечить их надлежащую функциональность, особенно в части технической поддержки.
Настоящим согласием Вы подтверждаете, что являетесь субъектом предоставляемых персональных данных, а также подтверждаете достоверность предоставляемых данных.
Компания «ТЕКОРА» предпринимает разумные меры для поддержания точности и актуальности имеющихся у нее персональных данных, а также удаления устаревших и других недостоверных или излишних персональных данных, тем не менее, Вы несёте ответственность за предоставление достоверных сведений, а также за обновление предоставленных данных в случае каких-либо изменений.
Вы можете в любой момент изменить (обновить, дополнить) предоставленную Вами персональную информацию или её часть, а также параметры её конфиденциальности путем обращения в Компанию «ТЕКОРА».
Обращаем внимание, что данное согласие предоставляется исключительно на добровольной основе. Настоящее согласие действует в течение 20 лет и может быть отозвано Вами в любое время, путем направления Компании «ТЕКОРА» заказного письма с уведомлением о вручении по адресам для корреспонденции Компании «ТЕКОРА», которые указаны в настоящем тексте согласия.
Все предложения или вопросы по поводу настоящей Политики следует сообщать Компании «ТЕКОРА» по телефону +7(495) 336-16-19 или по адресу электронной почты office@tekora.ru.
Политика конфиденциальности может обновляться в связи с возможными поправками к закону или изменениями внутренних процессов Компании «ТЕКОРА».
Последнее обновление: 1 марта 2021 г.