Соразмерность и рентабельность затрат
7. Функция и индикатор соразмерности
В мировой литературе интерес к замене диаграмм (кривых) Лоренца аналитическими функциями породил целый набор форм [10]. В нашем случае (см. пп. 6.1 – 6.5), учитывая близость диаграмм к окружности, мы использовали для аппроксимации соразмерности исходных данных функцию F(x,α) – производственную функцию с постоянной эластичностью замещения [11], [12].
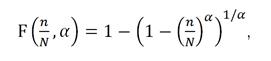
где α – индикатор соразмерности;
N – число значений в пакете затрат.
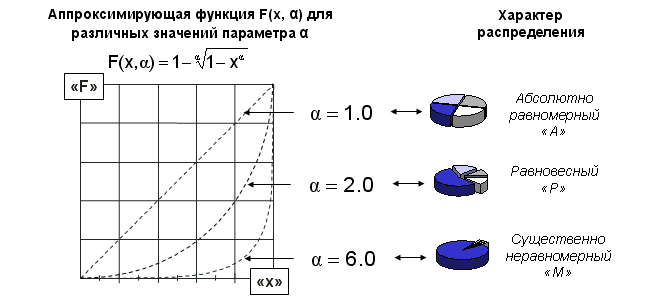
Рис. 14. Аппроксимирующая функция соразмерности F(x, α) для различных значений индикатора соразмерности (α)
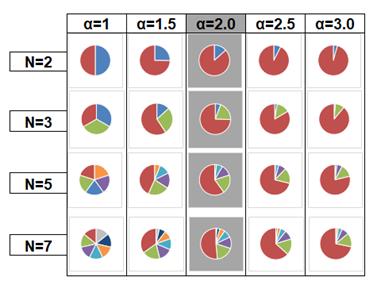
Удобство использования функции F(x, α) для аппроксимации широкого спектра диаграмм соразмерности подтверждается и возможностью варьировать форму функции соразмерности (см. Рис. 14) изменением только одного параметра α – индикатора соразмерности. Индикатор соразмерности позволяет упорядочивать долевые диаграммы с различным числом позиций N между двумя предельными случаями: «А» и «М» (Рис. 15).
Рис. 15. Упорядоченный ряд долевых диаграмм
Этого, однако, недостаточно для ответа на вопрос о предпочтительности диаграммы соразмерности с α=2.0. Для ответа на данный вопрос воспользуемся еще одним вариантом представления таблицы исходных данных в виде векторной диаграммы.
8. Векторная диаграмма затрат
Поясним представление таблицы затрат в виде вектора (Рис. 16) на простейшем примере (N=2).
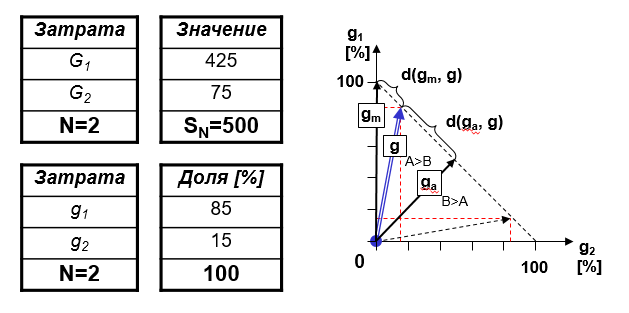
Рис. 16. Представление таблицы затрат в виде вектора
Векторное представление системы затрат позволяет рассчитать удаленности (d) конца фактического вектора (g) от концов крайних положений (gaи gm).
В общем случае расстояние d между концами произвольных векторов ![]() и
и ![]() :
: ![]() и
и ![]() в пространстве RN равно:
в пространстве RN равно:
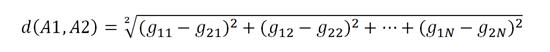
Во множестве соразмерностей систем затрат, представленных в виде векторов в пространстве RN, есть долевая диаграмма, расположенная на равном расстоянии от предельных по соразмерности вариантов «А»: ![]() и «М»:
и «М»: ![]() .
.
Покажем реализацию сделанного утверждения на примере пакетов затрат {g}, генерируемых с помощью функции соразмерности F(n/N, α):
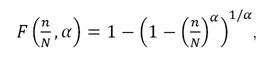
где α – индикатор соразмерности;
N – число значений в пакете затрат;
n – порядковый номер конкретной затраты в упорядоченном ряду затрат.
Причем доля конкретной затраты
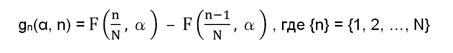
Результаты расчетов удаленностей для N=5 приведены на Рис. 17. Видно, что точка равновесия вариантов «А» и «М» реализуется при индикаторе соразмерности α=2.0.
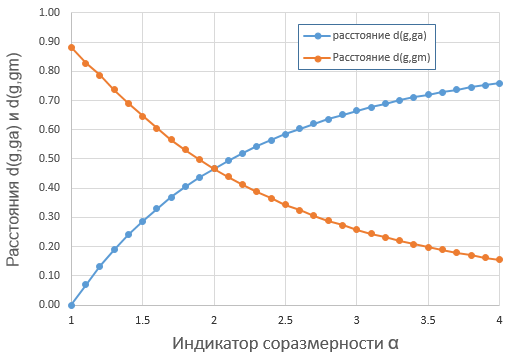
Рис. 17. Результаты расчетов удаленностей для модельного примера N=5
То есть, для N = 5 расстояние d(g, ga) и d(g, gm) между концом вектора ![]() и концами векторов
и концами векторов ![]() и
и ![]() в пространстве R5 при α = 2.0, соответственно, равны:
в пространстве R5 при α = 2.0, соответственно, равны:
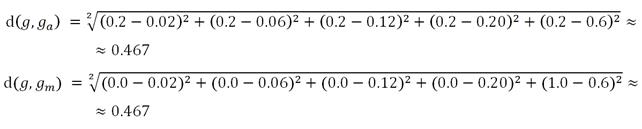
Настоящая Политика конфиденциальности персональных данных действует в отношении всех персональных данных, которые Компания «ТЕКОРА» может получить от Вас во время использования Вами сайтов компании.
Заполняя форму на сайте https://tekora.ru/ и других веб-сайтах Компании «ТЕКОРА», которые собирают данные и ссылаются на эти условия, Вы даете свое добровольное согласие Компании «ТЕКОРА» на обработку нижеследующих персональных данных с применением автоматизированных средств обработки или без таковых: фамилия, имя, отчество; место работы, наименование занимаемой должности; адрес электронной почты; номер контактного телефона.
Предоставляя Компании «ТЕКОРА» информацию, необходимую для инициирования дальнейшего взаимодействия, Вы выражаете согласие на ее использование в соответствии с настоящей Политикой.
Если Вы не согласны с приведенными в настоящем документе условиями, пожалуйста, не используйте данные веб-сайты и не заполняйте формы запроса информации.
Компания «ТЕКОРА» означает:
АО «ТЕКОРА», Юридический адрес: 119633, г. Москва, муниципальный округ Ново-Переделкино, Боровское ш., дом. 18, корп. 3, этаж 1, помещение 1, комната 5, офис 40.
Почтовый адрес: 117393, Москва, ул. Профсоюзная, д.56, оф. 15оф 19-23.
Под обработкой персональных данных понимаются действия, предусмотренные законодательством Российской Федерации, в том числе Федеральным законом от 27.07.2006 N 152-ФЗ. "О персональных данных".
Предоставляя свои персональные данные Вы соглашаетесь на их обработку, включая сбор, запись, систематизацию, накопление, хранение, уточнение (обновление, изменение), извлечение, использование, передачу, обезличивание, удаление, уничтожение Компанией «ТЕКОРА» в целях обработки Ваших заказов и запросов, для осуществления деятельности по продвижению товаров, работ, услуг или объектов интеллектуальной собственности на рынке путем осуществления прямых контактов с Вами с помощью средств связи, оценки и анализа сайта, анализа покупательских особенностей и предоставления персональных рекомендаций; информирования Вас об акциях, скидках и специальных предложениях посредством электронных рассылок, а также в целях связи с Вами (по электронной почте и/или телефону).
Предоставляя Компании «ТЕКОРА» свои персональные данные, вы можете быть уверены, что они не будут предоставляться третьим сторонам, за исключением случаев, когда это требуется в интересах деловых отношений между Вами и Компанией «ТЕКОРА». В некоторых случаях Компания «ТЕКОРА» обязана передавать Ваши персональные данные третьим лицам в связи с требованиями применимого законодательства. Например, это может быть в случае, когда существуют основания подозревать в совершении преступления или неправомерном использовании веб-сайта Компании «ТЕКОРА».
Вы можете в любой момент отказаться от получения сообщений по электронной почте, однако это не затрагивает передачу сообщений по электронной почте, которые требуются в целях реализации деловых отношений между Вами и компанией «ТЕКОРА».
Указанные веб-сайты содержат несколько ссылок на компании, с которыми Компания «ТЕКОРА» поддерживает деловые отношения. Компания «ТЕКОРА» не несет ответственность за соответствие требованиям по защите персональных данных в отношении использования веб-сайтов партнеров Компании «ТЕКОРА». Для получения информации о защите данных при посещении этих сайтов, пожалуйста, ознакомьтесь с политиками конфиденциальности на веб-сайтах соответствующих компаний.
Персональные данные, собираемые Компанией «ТЕКОРА», хранятся на защищенных серверах. Доступ разрешен только ограниченному числу уполномоченных лиц, которые нуждаются в нем для того, чтобы управлять веб-сайтами Компании «ТЕКОРА» или обеспечить их надлежащую функциональность, особенно в части технической поддержки.
Настоящим согласием Вы подтверждаете, что являетесь субъектом предоставляемых персональных данных, а также подтверждаете достоверность предоставляемых данных.
Компания «ТЕКОРА» предпринимает разумные меры для поддержания точности и актуальности имеющихся у нее персональных данных, а также удаления устаревших и других недостоверных или излишних персональных данных, тем не менее, Вы несёте ответственность за предоставление достоверных сведений, а также за обновление предоставленных данных в случае каких-либо изменений.
Вы можете в любой момент изменить (обновить, дополнить) предоставленную Вами персональную информацию или её часть, а также параметры её конфиденциальности путем обращения в Компанию «ТЕКОРА».
Обращаем внимание, что данное согласие предоставляется исключительно на добровольной основе. Настоящее согласие действует в течение 20 лет и может быть отозвано Вами в любое время, путем направления Компании «ТЕКОРА» заказного письма с уведомлением о вручении по адресам для корреспонденции Компании «ТЕКОРА», которые указаны в настоящем тексте согласия.
Все предложения или вопросы по поводу настоящей Политики следует сообщать Компании «ТЕКОРА» по телефону +7(495) 336-16-19 или по адресу электронной почты office@tekora.ru.
Политика конфиденциальности может обновляться в связи с возможными поправками к закону или изменениями внутренних процессов Компании «ТЕКОРА».
Последнее обновление: 1 марта 2021 г.